مقدمه
در نظریه مجموعه ها (set theory)
عملگری به نام "تفاضل متقارن" یا به انگلیسی Symmetric Difference
وجود دارد که تعریف آن به صورت زیر است (طبق تعریف
Wikipedia):
مجموعه عناصری که در یکی از دو جدول
A و B وجود دارند ولی جزء
اشتراکاتشان نیستند. تفاضل متقارن دو مجموعه را بصورت زیر نمایش می دهند:
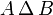
بطور نمونه اگر مجموعه ی A
شامل عناصر {3و2و1} و B
شامل اعضای {4,2,1} باشد تفاضل متقارن این دو، عناصر 4و3
خواهد بود.
نمودار Venn
تفاضل متقارن:
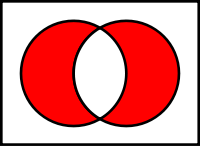
فرمول : اجتماع تفاضل A
از B و B از A
برابر با تفاضل متقارن است یعنی:
مساله
بعد از اینکه مقدمات بیان شد و شرایط
کمی بیشتر برای طرح مساله مساعد شد می تونیم به مساله بپردازیم.
فرض کنید در کلاسی دانشجویان این امکان را دارند که در دو رشته ورزشی فعالیت کنند.
هدف ما انتخاب دانشجویانی است که تنها در یک رشته ورزشی در حال فعالیت هستند (همراه
با رشته ورزشی در صورت تمایل).
برای این کار دو جدول در نظر می گیریم
که یکی لیست دانشجویانی که در رشته فوتبال هستند و جدول دیگر لیست دانشجویانی که در
رشته ورزشی ping-pong مشغول بازی هستند. توسط دو عبارت زیر
این دو جدول ساخته و تعداد سطر برای نمونه در آن می گسترانیم:
CREATE
TABLE PingPing
(
std_id INT
NOT NULL
PRIMARY KEY
);
CREATE
TABLE FootBall
(
std_id INT
NOT NULL
PRIMARY KEY
);
INSERT
INTO PingPing
VALUES (1),
(2),
(3);
INSERT
INTO FootBall
VALUES (1),
(2),
(4);
تفاضل متقارن داده های این دو جدول
شامل عناصر 3 و 4 خواهد بود.
راه حل
اگر ما منطق ای که در
تعریف تفاضل بکار رفته است را تبدیل به زبان SQL کنیم نتیجه
مورد نظر حاصل خواهد شد.
(--
A\B
SELECT std_id
FROM
PingPong
EXCEPT
SELECT
std_id
FROM
FootBall
)
UNION
(--
B\A
SELECT std_id
FROM
FootBall
EXCEPT
SELECT
std_id
FROM
PingPong
);